News
- Code release
- Improved version: CorticalFlow++: Boosting Cortical Surface Reconstruction Accuracy, Regularity, and Interoperability
CorticalFlow
In this paper, we introduce CorticalFlow, a new geometric deep-learning model that, given a 3-dimensional image, learns to deform a reference template towards a targeted object. To conserve the template mesh’s topological properties, we train our model over a set of diffeomorphic transformations. This new implementation of a flow Ordinary Differential Equation (ODE) framework benefits from a small GPU memory footprint, allowing the generation of surfaces with several hundred thousand vertices. To reduce topological errors introduced by its discrete resolution, we derive numeric conditions which improve the manifoldness of the predicted triangle mesh. To exhibit the utility of CorticalFlow, we demonstrate its performance for the challenging task of brain cortical surface reconstruction. In contrast to current state-of-the-art, CorticalFlow produces superior surfaces while reducing the computation time from nine and a half minutes to one second. More significantly, CorticalFlow enforces the generation of anatomically plausible surfaces; the absence of which has been a major impediment restricting the clinical relevance of such surface reconstruction methods.
Regular surface extraction for medical imaging
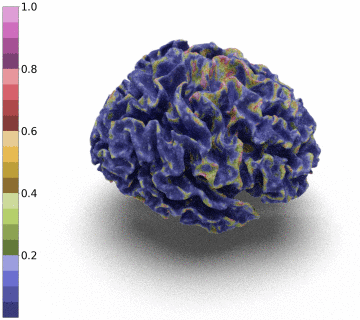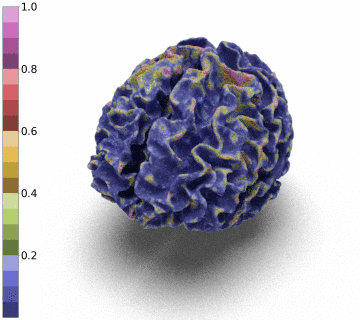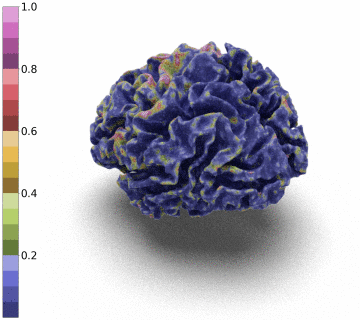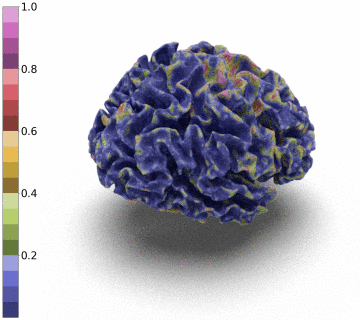
Surfaces of the cerebral cortex are a linchpin in neuroimaging studies (pial = outer surface and white = inner surface). From these surfaces, one can derive biomarkers as the thickness and gyrification can be used to track the development and aging of the brain but can also be used to detect numerous neurological pathologies.
Recently, medical surface only reconstruction methods have gained in momentum leveraging advanced tools of Deep-Learning, signed-distance functions and graph convolution models [1,2,3,4,5]. By bypassing the need for discrete 3D segmentation maps, these methods allow the reconstruction of more precise surfaces.
However, to be able to extract and co-register information onto the same average patient, the reconstructed surface has to be of genus zero. In this paper, we detail a method that leverages the Stationary Vector Fields (SVF) integration introduced by [6,7]. Since the data that we have to displace is not located on a Cartesian grid (in our case a triangle mesh), we detail an invertible resolution technique for resulting ODEs.
Moreover, we notice that the resulting deformation can be composed (3 times) to enhance the quality of the surface reconstruction while keeping a very acceptable memory footprint.
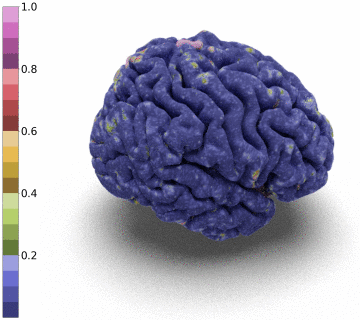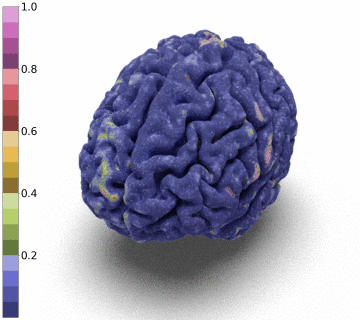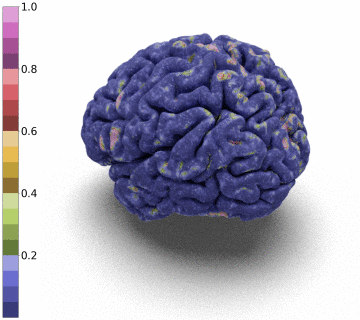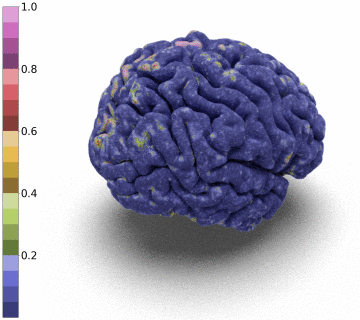




References
[1] Wickramasinghe, U., Remelli, E., Knott, G., & Fua, P. (2020, October). Voxel2mesh: 3d mesh model generation from volumetric data. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 299-308). Springer, Cham.
[2] Ma, Q., Robinson, E. C., Kainz, B., Rueckert, D., & Alansary, A. (2021, September). PialNN: A Fast Deep Learning Framework for Cortical Pial Surface Reconstruction. In International Workshop on Machine Learning in Clinical Neuroimaging (pp. 73-81). Springer, Cham.
[3] Hong, Y., Ahmad, S., Wu, Y., Liu, S., & Yap, P. T. (2021, September). Vox2Surf: Implicit Surface Reconstruction from Volumetric Data. In International Workshop on Machine Learning in Medical Imaging (pp. 644-653). Springer, Cham.
[4] Gopinath, K., Desrosiers, C., & Lombaert, H. (2021, September). SegRecon: Learning Joint Brain Surface Reconstruction and Segmentation from Images. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 650-659). Springer, Cham.
[5] Cruz, R. S., Lebrat, L., Bourgeat, P., Fookes, C., Fripp, J., & Salvado, O. (2021). Deepcsr: A 3d deep learning approach for cortical surface reconstruction. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (pp. 806-815).
[6] Vincent Arsigny. Processing Data in Lie Groups : An Algebraic Approach. Application to Non-Linear Registration and Diffusion Tensor MRI. Human-Computer Interaction [cs.HC]. Ecole Polytechnique X, 2006. English. ⟨tel-00121162⟩
[7] Ashburner, J. (2007). A fast diffeomorphic image registration algorithm. Neuroimage, 38(1), 95-113.
If you find this work useful, please cite
@InProceedings{Lebrat:NIPS21:CorticalFlow,
author = {Lebrat, Leo and Santa Cruz, Rodrigo and de Gournay, Frederic and Fu, Darren and Bourgeat, Pierrick and Fripp, Jurgen and Fookes, Clinton and Salvado, Olivier},
title = {CorticalFlow: A Diffeomorphic Mesh Deformation module for Cortical Surface Reconstruction},
booktitle = {Advances in Neural Information Processing Systems},
volume = {34},
year = {2021},
month = {December},
year = {2021}
}
@article{santacruz2022cfpp,
title = {CorticalFlow++: Boosting Cortical Surface Reconstruction Accuracy, Regularity, and Interoperability},
author = {Santa Cruz, Rodrigo and Lebrat, Leo and Fu, Darren and Bourgeat, Pierrick and Fripp, Jurgen and Fookes, Clinton and Salvado, Olivier},
journal = {Arxiv},
year = {2022}
}
Acknowledgment
This research was supported by Maxwell plus











