MongeNet

Recent advances in geometric deep-learning introduce complex computational challenges for evaluating the distance between meshes. From a mesh model, point clouds are necessary along with a robust distance metric to assess surface quality or as part of the loss function for training models. Current methods often rely on a uniform random mesh discretization, which yields irregular sampling and noisy distance estimation. We introduce, a fast and optimal transport based sampler that allows for an accurate discretization of a mesh with better approximation properties.

Mesh Sampling Example

The images below show an airplane mesh with sampled point clouds using MongeNet and Random Uniform Sampling. We can observe that random uniform sampling produces clustering of points (clamping) along the surface resulting in large undersampled areas and spurious artifacts. In contrast, MongeNet sampled points are uniformly distributed which better approximate the underlying mesh surfaces.

Plane of the ShapeNet dataset sampled with 5k points. Left: Point cloud produced by MongeNet. Right: Point cloud produced by the random uniform sampler. Note the clamping pattern across the mesh produced by the random uniform sampling approach.

The edge provided by MongeNet can be better visualized on the small set of faces along with the Voronoi tessellation associated to the point cloud and displayed below. In contrast to uniform random sampling, MongeNet samples points that are closer to the input mesh in the sense of the 2-Wasserstein optimal transport distance. This translates into a uniform Voronoi diagram.

Discretization of a mesh by a point cloud. Left: MongeNet discretisation. Right: Classical random uniform, with in red the resulting Voronoi Tessellation spawn on the triangles of the mesh.

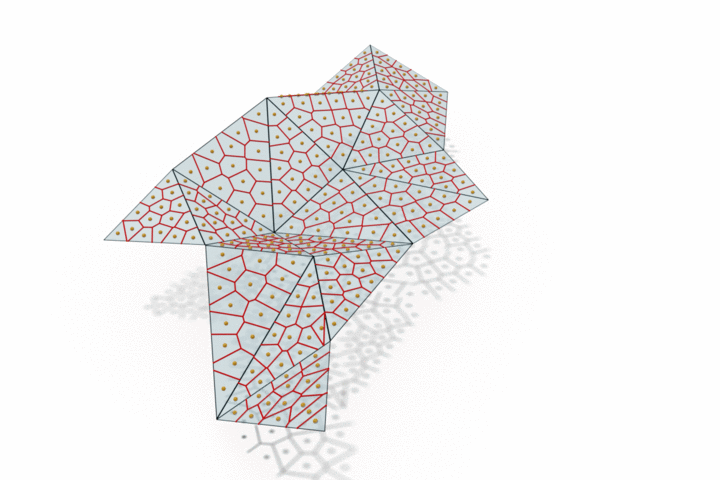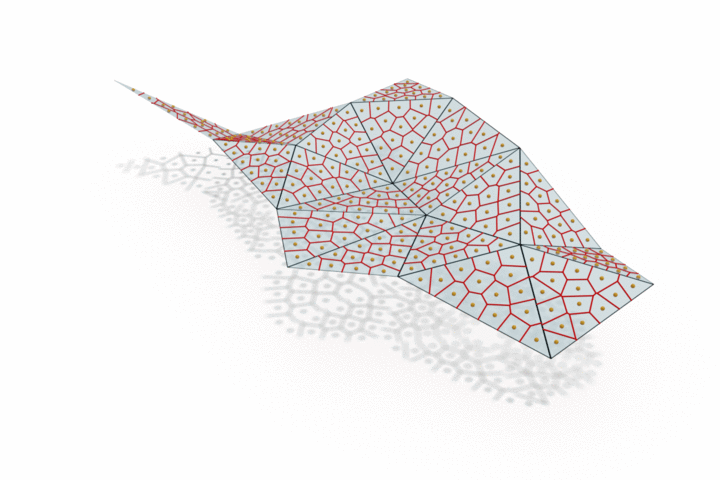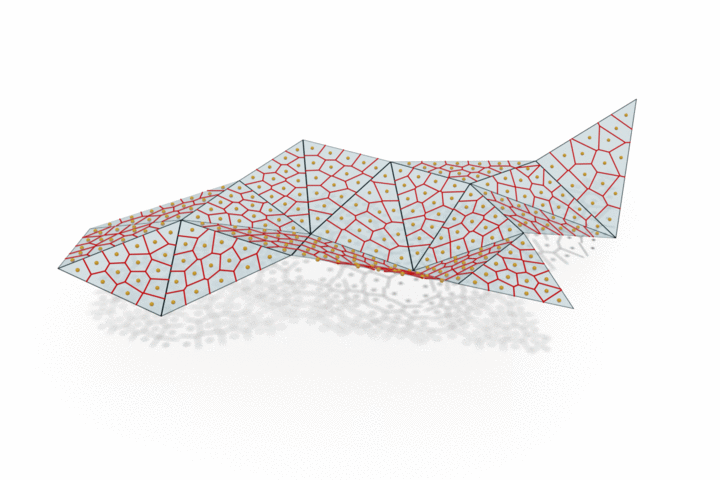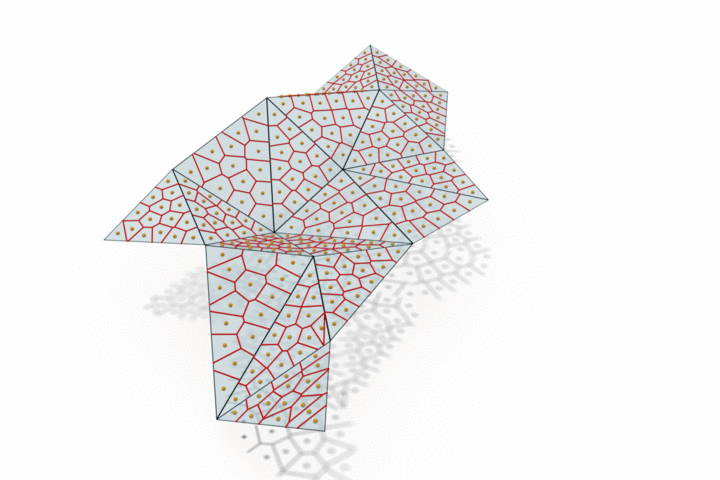
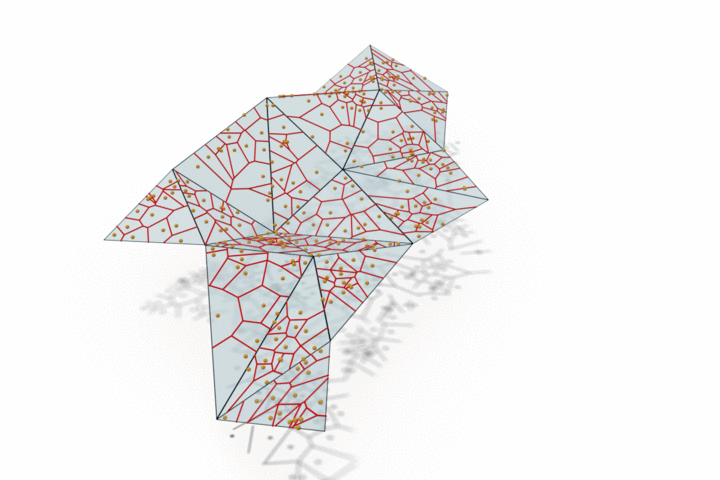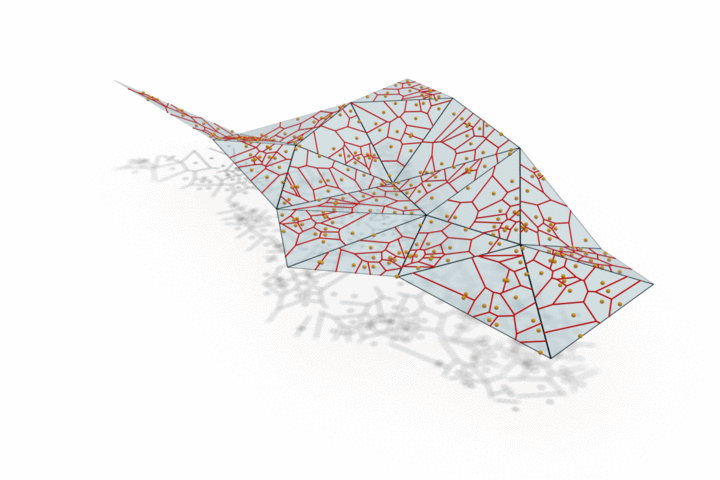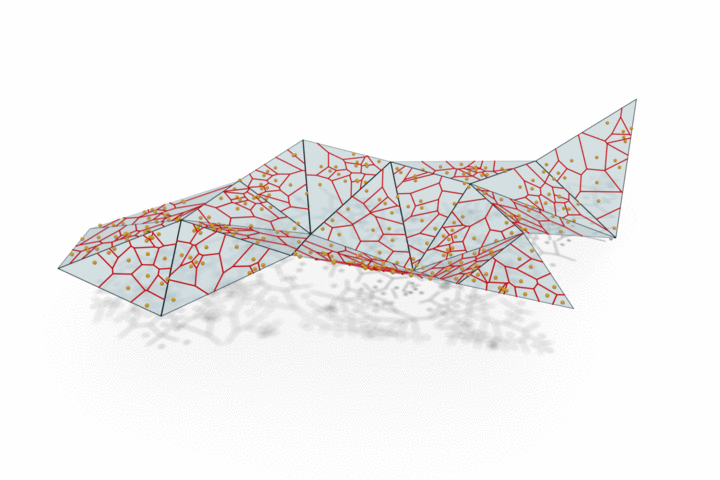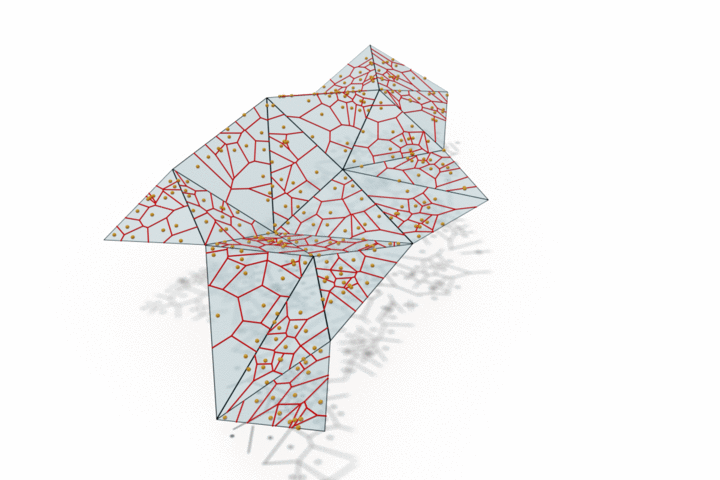
Reconstructing watertight mesh surface from noisy point cloud

The videos below display the benefit of using MongeNet in a learning context. It compares the meshes reconstructed with Point2Mesh model using MongeNet and Random Uniform Sampling for two very complex shapes. MongeNet produces better results, especially for the shape’s fine details and areas of high curvature.

If you find this work useful, please cite

@InProceedings{Lebrat:CVPR21:MongeNet,
    author    = {Lebrat, Leo and Santa Cruz, Rodrigo and Fookes, Clinton and Salvado, Olivier},
    title     = {MongeNet: Efficient sampler for geometric deep learning},
    booktitle = {Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
    month     = {June},
    year      = {2021}
}

Acknowledgment

This research was supported by Maxwell plus